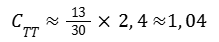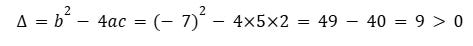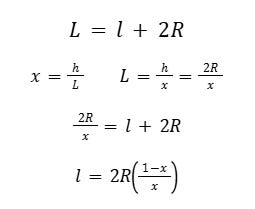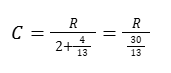Exclusivo / Ing. G. Pierrez: La geometría oculta del caso del UAP Nimitz

El ingeniero Guillaume Pierrez ha encontrado una proporción intrigante en las proporciones del ovni «TicTac».

Una forma que no tiene en cuenta la aerodinámica

Durante una carrera de Fórmula 1, ¿estaría dispuesto a apostar a que un participante se presenta con ruedas cuadradas? Probablemente no...
Sin embargo, esta es casi la clase de apuesta que los diseñadores del TIC TAC (si es que hay un diseño) podrían haber hecho.
Como parte de un proyecto de diseño de aeronave supersónica, cualquier ingeniero aeronáutico comenzaría con una forma de punta de flecha. Esto es, de hecho, lo que recomienda la mecánica de fluidos para promover el flujo de aire y minimizar el calentamiento del fuselaje. Por lo tanto, es completamente inverosímil optar por la forma de un TIC TAC para un móvil con esta capacidad.
Aunque no conocemos su técnica de vuelo, ya sabemos una cosa esencial: la forma parece prevalecer sobre la aerodinámica.

¿Es el fenómeno el resultado de un diseño?

Antes de continuar, conviene confirmar o refutar la artificialidad del fenómeno. Algunos argumentarán con razón que el comportamiento descrito por los testigos, la cinética y muchos otros aspectos no dejan lugar a dudas sobre la naturaleza artificial del fenómeno. Es cierto que todos estos elementos constituyen un conjunto de presunciones muy sólido.
Sin embargo, creo que es posible un enfoque más técnico y objetivo. Permítanme explicarlo usando una lata de refresco:

Piense en su lata de refresco de aluminio. Piense por un momento en quienes la diseñaron y en la primera pregunta que tuvieron que hacerse:
«¿Qué dimensiones proporcionan un volumen óptimo con un coste mínimo de aluminio? »
Si consideramos que una lata es aproximadamente comparable a un cilindro, podemos describir su volumen y su superficie basándonos en su radio R y su altura h. A continuación, establecemos una relación entre volumen, coste y superficie. Sin entrar en detalles, las matemáticas nos permiten encontrar la solución ideal.
Al hacerlo, la lata resultante lleva literalmente el «rastro matemático» de su artificialidad en sus dimensiones:
Ahora imagina a un arqueólogo del futuro que encuentra los restos de tu lata. Podrá medir las dimensiones y llevará a cabo el razonamiento inverso para ver finalmente con certeza el esfuerzo de optimización. Porque hay un gran número de posibilidades, ¡pero solo una está optimizada! Lógicamente, concluirá que este objeto fue diseñado y producido por personas inteligentes.

Por lo tanto, si consideramos que el objeto es artificial y está inteligentemente diseñado, tal vez sea posible encontrar un «rastro de optimización» en su geometría y sus dimensiones, al igual que nuestro arqueólogo pudo encontrar un rastro de optimización en la forma de nuestra lata... Por el contrario, si no encontramos nada concluyente, el misterio seguirá sin resolverse...
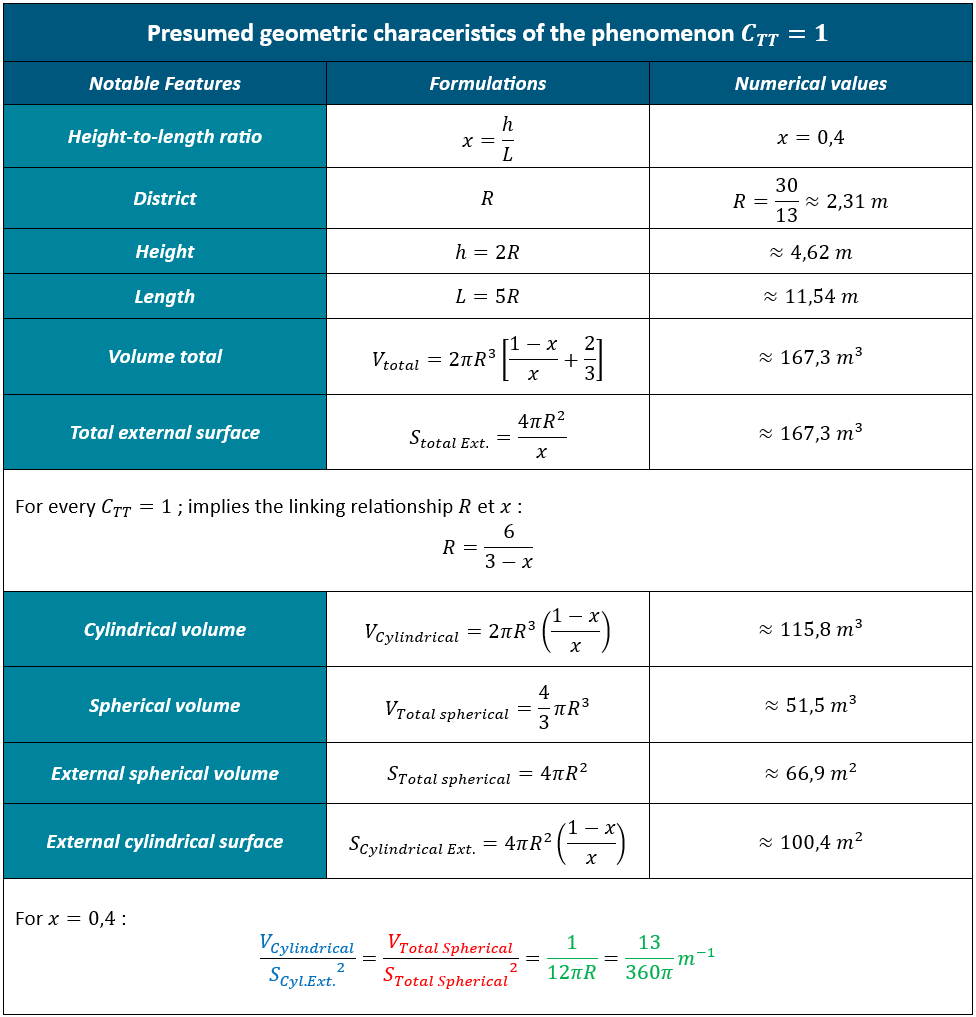
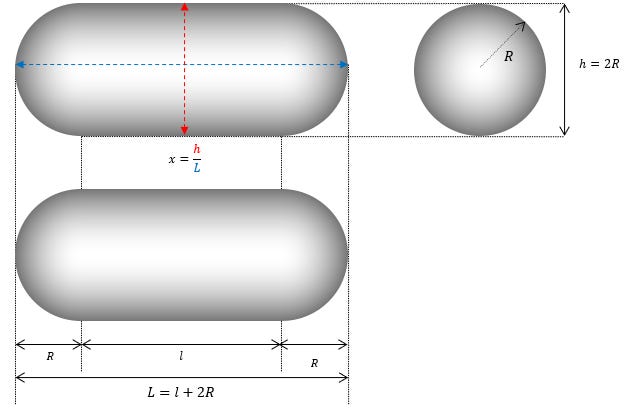
Para empezar, tenga en cuenta que la forma de un TIC TAC requiere solo dos parámetros (R y x) para definir todas las soluciones posibles:

En esta etapa podemos ver que la geometría del fenómeno incluye dos tipos de superficies distintas:
Esta observación puede parecer trivial, pero resultará esencial más adelante.

• Una superficie cilíndrica (el lado del cilindro aparece en azul)

• Dos superficies esféricas (semiesferas en los extremos en rojo)

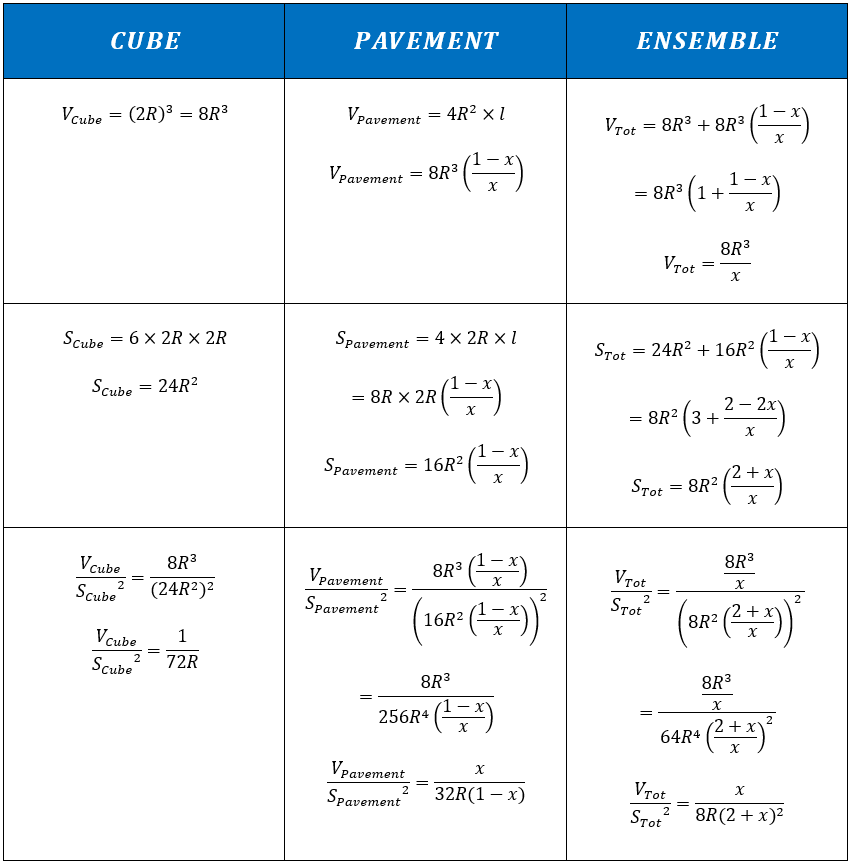
Ahora, describamos matemáticamente los volúmenes y superficies de cada una de estas partes y compárenlos entre sí utilizando una matriz (los detalles de los cálculos están disponibles en el anexo 2:

De este desarrollo no se desprende nada en particular. De hecho, cuando R y x son indeterminados, no parece surgir claramente ninguna relación concluyente.
Probemos ahora el mismo enfoque introduciendo uno de los dos valores R o x. No es posible dar una estimación de R que sea suficientemente precisa, por otro lado, basándonos en las imágenes visibles del vídeo FLIR 1, es posible proporcionar un marco para x:
Las imágenes del espectro visible son más precisas que las imágenes del espectro IR que tienden a «desbordarse».

Volvamos a nuestra tabla anterior con x=0,4:

Para el valor de x=0,4, la matriz de comparación revela ahora una relación singular que vincula los volúmenes y las superficies de las partes:

Que también puede escribirse de forma más elegante:

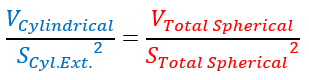
Por conveniencia, esta relación se denominará V/S² para la continuación del estudio.
En esta etapa, solo se puede afirmar que la forma observada realmente presenta una relación geométrica singular, que solo aparece para la relación altura-longitud observada, es decir, Para x=0,4, verificación disponible en el Anexo 3.

La resolución de la relación V/S² conduce a una solución particular para x que corresponde precisamente al valor observado en el video. Por lo tanto, es muy poco probable que esta solución particular aparezca por casualidad.
Esta observación tiende a demostrar que el objeto es, de hecho, el fruto de un diseño ingenioso cuya naturaleza podría estar vinculada a la relación V/S². Si este es realmente el caso, esta relación sería, por lo tanto, también el punto de partida para el diseño del fuselaje.
Veremos posteriormente que la relación es, en realidad, la consecuencia de una relación más general, lo que excluye de facto la posibilidad de una coincidencia. Sin embargo, hablar de ello aquí haría que el razonamiento fuera anacrónico.

¿Podría ser una coincidencia afortunada?

Por débil que sea, hay que considerar la posibilidad de una coincidencia, pero el nudo se aprieta de nuevo cuando estudiamos el aspecto de la compacidad:
La compacidad se define por la relación entre el volumen de un objeto y su superficie. Permite comparar la capacidad de las formas geométricas para abarcar un volumen máximo dentro de una superficie mínima.
A modo de ejemplo, la esfera es la forma más eficiente con una compacidad de:

Determinemos la compacidad de la forma TIC TAC:

Que, para x=2/5, se convierte en:

Ahora nos falta una estimación de R para dar un valor aproximado de CTT.
Recordemos que los pilotos estimaron la longitud del Tic-Tac en aproximadamente 40 pies o aproximadamente 12 m.
Recordemos también la definición de L en el diagrama: L=l+2R

Que para x=2/5 se convierte en:

Podemos entonces dar una estimación de la compacidad del Tic-Tac:

Este resultado no nos da ninguna certeza y solo permite especulaciones que son difíciles de verificar pero que, sin embargo, merecen ser presentadas.
La estimación de 40 pies de longitud dada por el piloto obviamente contiene una incertidumbre, a la que se suma la de la conversión de pies a metros. Por lo tanto, podemos preguntarnos razonablemente si la compacidad real no sería 1.
Si consideramos que:

Entonces:

La longitud sería entonces:

Lo que correspondería aproximadamente a 38 pies y resultaría compatible con la observación realizada por los pilotos. Sobre la base de esta hipótesis, podemos completar el diagrama inicial y arriesgarnos a dar una predicción aproximada de las dimensiones del fenómeno:

Por supuesto, es sorprendente observar que dos razonamientos distintos pueden conducir a predicciones concordantes, tanto con respecto al vídeo (valor de x=0,4) como a la estimación de la longitud de los pilotos (11,54 m frente a 12,19 m). Esta concordancia es, en sí misma, realmente desconcertante y tiende a priori a favor de un diseño juicioso.
A efectos prácticos, los valores numéricos de los demás aspectos geométricos se resumen a continuación:

Con esto concluye la primera parte.
La segunda parte resulta más difícil de explicar y mucho más matemática, pero también es la que, en mi opinión, es a la vez la más convincente y la más asombrosa.

¿Qué podemos aprender de la relación V/S²?

Recordemos la relación:

En esta forma no podemos aprender mucho más. Necesitamos introducir un nuevo aspecto como la expresión del volumen y la superficie del conjunto. La idea es simple y el resultado es muy fácil de demostrar (demostración disponible en el anexo 4):

Por lo tanto, obtenemos esta triple relación que nos enseña que, desde un punto de vista geométrico, el conjunto de la forma también está en relación con las diferentes partes. Obviamente, las restricciones son aún más específicas de lo que se imaginaba anteriormente.
También muestra el coeficiente 25/13... que, que yo sepa, no se corresponde con ninguna constante en física. A pesar de mis búsquedas en la literatura y en las hojas de trucos de ingeniería, no puedo encontrar ninguna correspondencia ni para la relación ni para el coeficiente 25/13.
Sin embargo, la relación permite «visualizar» un flujo (posiblemente de naturaleza electromagnética) que se intercambia entre los diferentes volúmenes a través de las diferentes paredes, pero se trata de una interpretación personal puramente especulativa. La motivación de esta relación podría ser estética, después de todo.
Si, como a mí, el proceso le parece interesante hasta ahora, ¡aquí es donde realmente se vuelve confuso! Le dejo que juzgue por sí mismo:
Te ahorraré los detalles personales que me llevaron a esta idea y te llevaré directamente a los resultados:

Después de innumerables intentos de averiguar más, consideré la posibilidad de que la relación no fuera exclusiva del TIC TAC. Así que apliqué la relación a otras formas «geométricamente vecinas». Dejaré que juzgues los resultados:

(Los detalles de los cálculos para cada forma están disponibles en el anexo 5)
Al aplicar la relación a diferentes formas, obtenemos diferentes valores para x, ¡pero seguimos encontrando el mismo coeficiente 25/13! Por lo tanto, parece que lo que inicialmente consideramos una relación específica de una sola forma geométrica es, en realidad, un principio aplicable a diferentes formas.
Por conveniencia, me permití llamarlo «Principio de Afinidad Geométrica» o PAG en referencia a una tercera parte inacabada.
A día de hoy, estoy considerando la posibilidad de que este principio permita categorizar las formas según sus simetrías. Quizá sería posible categorizar la familia 25/13 u otras familias aún por descubrir. El origen de este principio también podría provenir de una consecuencia de los grupos LIE o incluso de la aplicación de un lagrangiano a una relación aún indeterminada.
Sea como fuere, el Principio de Afinidad Geométrica es un objeto matemático puro e independiente del fenómeno que nos pone tras su pista. Se trata de un problema matemático en sí mismo y debe abordarse, explorarse y analizarse como tal. La forma del TIC TAC sería al parecer solo una aplicación del Principio de Afinidad Geométrica. Interesarse en el único caso del TIC TAC puede, por lo tanto, compararse con observar solo una cara de un dado cuyo tamaño real aún desconocemos.
Sin embargo, sigue siendo asombroso e incluso impactante que la simple curiosidad matemática aplicada a un caso de FANI pudiera haber llevado a tal descubrimiento...
Nos preguntamos cuál es la naturaleza de la ventaja que pudo haber prevalecido sobre la aerodinámica. Dado que este trabajo no ha sacado a la luz ninguna constante de la física hasta ahora, y que la literatura no menciona la relación, no podemos vincular nuestra relación con ninguna necesidad física o técnica. A pesar de los importantes avances, este aspecto sigue siendo un enigma.

Anexo 1: Cálculo

Anexo 2: Volúmenes y superficies de cada parte y del conjunto

Anexo 3: Verificaciones de la relación V/S²

Para el valor de x=0,4 y solo para este valor, la tabla de comparación revela una relación notable específica de la geometría de Tic-Tac:

Volviendo a nuestra primera tabla (antes de que no se tenga en cuenta el valor de x=0,4) podemos establecer la ecuación inicial:

Tenga en cuenta que esta relación es independiente de R y depende solo de x.
¿Cuáles son las soluciones de esta relación? Al expandir obtenemos:

Entonces

lo que da la ecuación cuadrática:

Entonces, para la forma

cuyo discriminante se escribe:

deducimos las raíces:

Por lo tanto, encontramos x=0,4 en perfecto acuerdo con las observaciones del video FLIR1

Solución esférica (corresponde a una solución donde l=0)
La resolución de la relación V/S² conduce a una solución particular para x que corresponde precisamente al valor observado en el vídeo. Por lo tanto, es muy poco probable que esta solución particular aparezca por casualidad.

Anexo 4: Extensión de la relación V/S²

Calculemos las relaciones indicadas en la primera columna antes de expresarlas según la superficie o el volumen del TIC TAC en la segunda columna:

Utilizando estas nuevas expresiones y recordatorios, expresemos los términos de la relación V/S2 en función de STT y VTT:

Al aplicar la relación V/S², obtenemos:

Verifiquemos para qué valor(es) de x la igualdad entre el ^tercer y el ^quinto término es válida resolviendo:

Encontramos concordantemente el valor x=0,4; lo que apoya nuestras hipótesis y deducciones anteriores. Ahora calculemos el valor de los términos:

Se demuestra así que para el valor particular x=0,4; podemos aplicar la relación:

Tenga en cuenta que esta formulación no presupone en modo alguno el valor de R.

Anexo 5: Aplicaciones de cálculos del principio de afinidad geométrica a diferentes formas

Recordemos la esquematización del fenómeno:

Recordemos la expresión de l:

En la primera parte, destacamos el valor particular x:

La igualdad de la afinidad geométrica entre las partes está, por lo tanto, sujeta a la condición x=2/5.
Comparemos ahora la afinidad geométrica del todo con las de cada parte:

Concluimos que para la forma del Tic-Tac, la relación de afinidad geométrica se escribe:

PRISMA DE SECCIÓN CUADRADA

Como en el caso del Tic-Tac, solo se tiene en cuenta la superficie que da al exterior.

¿Para qué valor de x podemos observar la igualdad de afinidades geométricas entre las partes?:

Comparemos la afinidad geométrica del todo con las de cada parte:

De una manera absolutamente asombrosa, encontramos la relación de afinidad geométrica con el mismo factor 25/13:

¿Correspondería la relación 25/13 a una constante hacia la cual convergen las afinidades geométricas bajo ciertas condiciones?
A efectos prácticos, se añaden algunas observaciones interesantes:
Calculemos la compacidad:

Para x=4/13:

De ello se deduce que si la compacidad es 1, entonces R vale 30/13 exactamente como en el caso del Tic-Tac...
Es muy sorprendente encontrar tantos resultados comunes entre dos formas tan diferentes.
Obsérvese también que:

CILÍNDRICO
La forma recuerda a ciertos casos de UAP en forma de «cigarro».
Esquematice la forma así:

Como en el caso del Tic-Tac, solo se tiene en cuenta la superficie que mira hacia el exterior.

Para qué valor de x podemos observar la igualdad de las afinidades geométricas de las partes:

Comparemos la afinidad geométrica del conjunto con las de cada parte:

Igual de sorprendente, volvemos a encontrar la relación de afinidad geométrica con el mismo factor 25/13:

A efectos prácticos, se añaden algunas observaciones interesantes:
Calculemos la compacidad:

Como aquí también, x=4/13:

Del mismo modo, si C=1, entonces R=30/13, una vez más exactamente como en el caso del Tic-Tac.
Sorprendentemente, resulta que la compacidad del cilindro es exactamente la misma que la del adoquín de sección cuadrada anterior.
PRISMA CON SECCIÓN HEXAGONAL
Esquemática la forma de esta manera:

Como en los casos anteriores, sólo se tiene en cuenta la superficie que da al exterior.

En estas condiciones, el radio interno del hexágono vale:

Para qué valor de x podemos observar la igualdad de las afinidades geométricas de las partes:

Comparemos la afinidad geométrica del conjunto con las de cada parte:

Con el mismo asombro, volvemos a encontrar la relación de afinidad geométrica con el mismo factor 25/13:

Solo el último término parece sugerir una variación en función de la forma geométrica. Es muy sorprendente observar el éxito de la relación de afinidad geométrica en estas pocas pruebas.
A efectos prácticos, se añaden algunas observaciones interesantes:
Calculemos la compacidad:

Ya que aquí también x=4/13:

Del mismo modo, si C=1, entonces R=30/13, una vez más exactamente como en el caso del Tic-Tac.
Sorprendentemente, resulta que la compacidad del prisma hexagonal es exactamente la misma que la del bloque cuadrado y el cilindro triple.